티스토리 뷰
보안을 하면서 Http를 Https로 바꾼다고 해커로부터의 공격에서 안전하지 않을수도 있다는것을 알았다. Https를 구성하고 안전한 프로토콜을 사용해야만 한다는 사실도 알았다. 그리고, Https를 구성하기 위해 서버와 서버, 서버와 클라이언트 사이에서 서로를 인증할 인증서와 인증키가 필요하다. 보안을 한다는건 서버와 클라이언트 또는 서버와 서버끼리 데이터를 주고 받을때 데이터를 암호화시켜 해커로부터 공격을 받더라도 해커가 데이터의 내용을 알수 없도록하여 데이터 유출이나 피해를 막는데 그목적이 있다. 이때 데이터를 어떻게 암호화를 시킬것인지에 대한 프로세스를 우리는 암호화 알고리즘이라고 부른다.

암호화 알고리즘을 이용하여 서버와 클라이언트 사이에서 사용할 인증서와 인증키를 생성하기도 하고, 데이터베이스의 인증 패스워드를 암호화시키기도 한다. 이 과정에서 우리는 데이터를 어떤 암호화 알고리즘을 선택하여 암호화를 할지 결정하는데 이때 사용하는 암호화 알고리즘에 MD5, SHA1, SHA2와 같은 알고리즘이 존재를 한다. 그래서 오늘은 어떤 알고리즘을 권장하는지 그렇지 않은 알고리즘은 어떤것인지 왜 사용을 해야하고 왜 사용을 하면 안되는지를 알아보았다.
아래 그림은 어떤 방법으로 암호화를 했느냐에 따른 결과를 보여주는 그림으로 MD5보다는 SHA1이 좀 더 암호화가 복잡하고, SHA1보다 SHA256이 암호화가 더 복잡하다는 걸 알 수 있다. 암호화 알고리즘 역시 오래된 기술이기 때문에 검색을 통해 많은 자료들을 찾아볼수 있다.

MD5
MD5(Message-Digest algorithm 5)는 128비트 암호화 해시 함수이다. RFC 1321로 지정되어 있으며, 주로 프로그램이나 파일이 원본 그대로인지를 확인하는 무결성 검사 등에 사용된다. 1991년에 로널드 라이베스트가 MD4를 대체하기 위해 고안했다. 그러나, 1996년에 MD5의 설계상 결함이 발견되었다. 이것은 매우 치명적인 결함은 아니었지만, 암호학자들은 해시 용도로 SHA-1과 같이 다른 안전한 알고리즘을 사용할 것을 권장하기 시작했다. 2004년에는 더욱 심한 암호화 결함이 발견되었고. 2006년에는 노트북 컴퓨터 한 대의 계산 능력으로 1분 내에 해시 충돌을 찾을 정도로 빠른 알고리즘이 발표되기도 하였다. 현재는 MD5 알고리즘을 보안 관련 용도로 쓰는 것은 권장하지 않으며, 심각한 보안 문제를 야기할 수도 있다. 2008년 12월에는 MD5의 결함을 이용해 SSL 인증서를 변조하는 것이 가능하다는 것이 발표되었다.
SHA
SHA(Secure Hash Algorithm, 안전한 해시 알고리즘) 함수들은 서로 관련된 암호학적 해시 함수들의 모음이다. 이들 함수는 미국 국가안보국(NSA)이 1993년에 처음으로 설계했으며 미국 국가 표준으로 지정되었다. SHA 함수군에 속하는 최초의 함수는 공식적으로 SHA라고 불리지만, 나중에 설계된 함수들과 구별하기 위하여 SHA-0이라고도 불린다. 2년 후 SHA-0의 변형인 SHA-1이 발표되었으며, 그 후에 4종류의 변형, 즉 SHA-224, SHA-256, SHA-384, SHA-512가 더 발표되었다. 이들을 통칭해서 SHA-2라고 하기도 한다.
SHA-1은 SHA 함수들 중 가장 많이 쓰이며, TLS, SSL, PGP, SSH, IPSec 등 많은 보안 프로토콜과 프로그램에서 사용되고 있다. SHA-1은 이전에 널리 사용되던 MD5를 대신해서 쓰이기도 한다. 혹자는 좀 더 중요한 기술에는 SHA-256이나 그 이상의 알고리즘을 사용할 것을 권장한다. SHA-0과 SHA-1에 대한 공격은 이미 발견되었다. SHA-2에 대한 공격은 아직 발견되지 않았으나, 전문가들은 SHA-2 함수들이 SHA-1과 비슷한 방법을 사용하기 때문에 공격이 발견될 가능성이 있다고 지적한다. 미국 표준 기술 연구소(NIST)는 SHA-3로 불리는 새로운 암호화 해시 알고리즘에 대한 후보를 공모하였다.
SHA-256
SHA-256은 현재가장 많은 분야에서 채택하여 사용되고 있는 암호 방식이다. 출력 속도가 빠르다는 장점을 갖고 있다. 또한 단방향성의 성질을 띄고 있는 암호화 방법으로 복호화가 불가능하다. SHA-384, 512, SHA-3보다는 유효 보호 수준이 낮을 지는 모르지만, 현재까지 안정성 문제에서도 큰 단점이 발견되지 않았고, 속도가 빠르기 때문에 인증서, 블록체인 등 많이 사용되고있으며, SHA-2라고 하면 SHA-256이라고 말할 정도로 상용화가 잘 되어있다.

* 단방향 알고리즘
단방향(One-Way) 암호화는 평문을 암호화했을 때 다시 평문으로 복호화할 수 없는 암호화이다. 대표적으로 많이 사용되는 알고리즘이 SHA-256 암호화 알고리즘이다. SHA-256은 임의의 길이 메시지를 256 비트(bits)의 축약된 메시지로 만들어내는 해시 알고리즘이다. 데이터의 수정과 변경을 검출 할 수 있으나 인증은 불가능하다. 인증에 사용하기 위해 메시지 인증 코드와 디지털 서명이 요구된다.
* 안정성
SHA-1은 구글 클라우드 서버를 기반으로 수행된 연구 사례에서 약 900경의 해시 연산을 통해 충돌이 발견된 경험이 있다. 이것을 바탕으로 근본적인 차이가 많이 없는 SHA-256의 안정성이 얼마나 높고 유지될 수 있다고 언급하기에는 어려움이 있다. 하지만 실질적으로 해시 취약점을 대상으로 하는 양자 컴퓨터가 출시되지 않는 이상 최소 근 10년가량은 안전하다는 판단할 수 있다. SHA-256의해 제공되는 해시 알고리즘은 일정한 컴퓨터 연산 속도의 향상을 염두에 둔 가정에도 산술적으로 매우 강력하다는 결론에 도달하게 된다.
이렇게 해서 MD5와 SHA1, SHA256에 대해 간략하게 알아보았다. 너무 어려워서 이해가 가질 읺지만 적어도 암호화 알고리즘에서 어떤 것이 주로 사용되는지는 알수 있을것 같다. 이 외에도 RSA나 DSA, ED25519와 같은 해시 알고리즘에 대해서도 알아보았다.
RSA
RSA는 공개키 암호시스템의 하나로, 암호화뿐만 아니라 전자서명이 가능한 최초의 알고리즘으로 알려져 있다. RSA가 갖는 전자서명 기능은 인증을 요구하는 전자 상거래 등에 RSA의 광범위한 활용을 가능하게 하였다. RSA는 두 개의 키를 사용한다. 여기서 키란 메시지를 열고 잠그는 상수(constant)를 의미한다. 일반적으로 많은 공개키 알고리즘의 공개키(public key)는 모두에게 알려져 있으며 메시지를 암호화(encrypt)하는데 쓰이며, 암호화된 메시지는 개인키(private key)를 가진 자만이 복호화(decrypt)하여 열어볼 수 있다. 하지만 RSA 공개키 알고리즘은 이러한 제약조건이 없다. 즉 개인키로 암호화하여 공개키로 복호화할 수도 있다. 공개키 알고리즘은 누구나 어떤 메시지를 암호화할 수 있지만, 그것을 해독하여 열람할 수 있는 사람은 개인키를 지닌 단 한 사람만이 존재한다는 점에서 대칭키 알고리즘과 차이를 가진다.
DSA
디지털 서명 알고리즘(Digital Signature Algorithm, DSA)은 디지털 서명을 위한 연방 정보 처리 표준이다. 1991년 8월 미국 국립표준기술연구소(NIST)는 자신들의 디지털 서명 표준(Digital Signature Standard, DSS)에 사용하기 위해 DSA를 제안했으며 1993년 FIPS 186로 채택되었다.
ED25519
Ed25519는 SHA-512 및 Curve25519를 사용한 EdDSA 서명 체계이다. 또한 Ed25519는 몇 가지 매력적인 기능을 갖춘 공개 키 서명 시스템이다. Ed25519 시그니처는 타원 곡선 시그니처로 여러 수준의 설계 및 구현에서 신중하게 엔지니어링되어 보안을 손상시키지 않으면서 매우 빠른 속도를 달성한다.
- 빠른 단일 서명 확인 (Fast single-signature verification)
- 매우 빠른 배치 검증 (Even faster batch verification)
- 빠른 키 생성(Fast key generation)
- 높은 보안 수준(High security level)
- 완전 방지 세션 키(Foolproof session keys)
- 충돌 탄력성(Collision resilience)
- 비밀 배열 인덱스가 없음(No secret array indices)
- 비밀 지점 조건이 없음(No secret branch conditions)
- 작은 서명(Small signatures)
- 작은 키(Small keys)
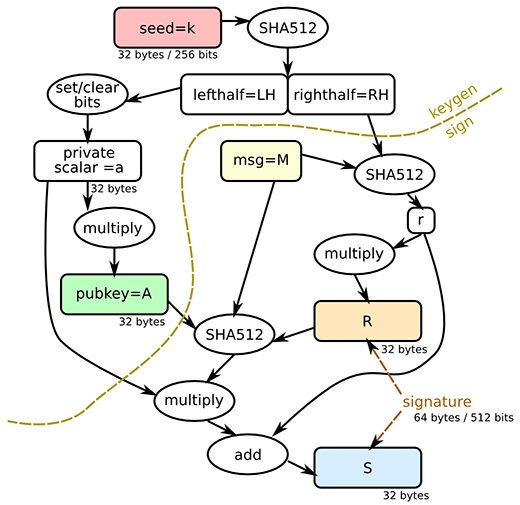
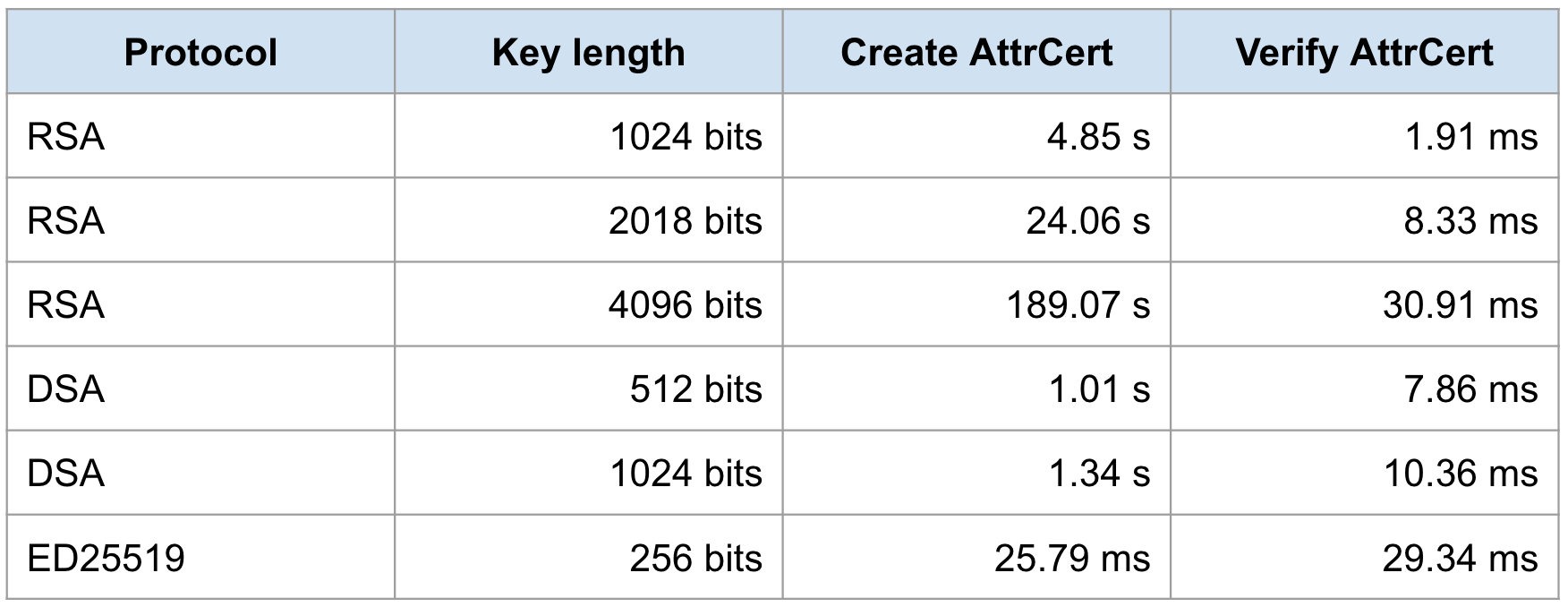
위에 보이는 그림이 Ed25519에 대한 알고리즘을 그림으로 표현한 것이며 아래표에서는 많이 사용하는 RSA나 DSA에 비해 ED25519가 얼마나 성능상 우수한지를 보여준다.
* EdDSA
공개 키 암호화에서 Edwards-curve EDDSA (Digital Signature Algorithm)는 트위스트 에드워드 곡선(Twisted Edwards curve)을 기반으로하는 Schnorr 서명의 변형을 사용하는 디지털 서명 체계이다. 보안을 유지하면서 기존 디지털 서명 체계보다 더 빠르도록 설계되었다.
* Twisted Edwards curve
대수 기하학에서 트위스트 에드워드 곡선(Twisted Edwards curve)은 타원 곡선의 평면 모델로, 2008 년에 Bernstein, Birkner, Joye, Lange 및 Peters가 도입 한 Edwards 곡선의 일반화다. 이 곡선 세트는 수학자 Harold M. Edwards의 이름을 따서 명명되었으며, 타원 곡선은 공개 키 암호화에서 중요하며 트위스트 에드워즈 곡선은 EdDSA라는 전자 서명 체계의 핵심이며 다른 디지털 서명 체계에서 발생하는 보안 문제를 피하면서 고성능을 제공한다.
참조링크
https://jusungpark.tistory.com/34
https://ko.wikipedia.org/wiki/SHA
https://ko.wikipedia.org/wiki/MD5
https://waytomine.com/sha-256-algorithm-function-bitcoin-network/
https://blog.webernetz.net/ssh-key-fingerprints/
https://www.keycdn.com/support/sha1-vs-sha256
처음 SHA256이나 ED25519는 데이터베이스 보안을 하면서 들었던 용어였다. 그런데, 이번에 이런 보안 용어들을 공부하면서 보니 이것이 데이터베이스 뿐이 아니라, 일반 SSH나 Http 보안에서 인증키를 만들때 사용하는 보안 알고리즘이라는 것을 알았다. 그리고, ED25519와 같은 경우에는 일반 보안 알고리즘과는 다르게 CPU와 같은 하드웨어 인프라 보안 단에서 사용하는 매우 고 난이도의 알고리즘이라는 것도 알았다. 그리고, 이런 보안 알고리즘들은 매우 다양한 보안 분야에서 쉽게 들을 수 있는 용어였다. 처음엔 각각 별개의 기술인 줄 알았지만, 하나씩 하나씩 보다보니 모든 기술들이 서로서로 연결되어 있고, 서로서로 연관되어 있다는 사실을 알았다. SNS의 친구의 친구처럼 말이다. 이로써 그렇게 어렵게만 느껴지던 보안 용어들이 이제는 어떻게 해서 만들어졌고, 지금은 어떤 보안 기술들을 많이 사용하는지는 적어도 내가 지금 쓰고 있는 시스템의 보안 기술들은 어떤것인지는 알 수 있게 되었다.
'OpenStack' 카테고리의 다른 글
| SDN and OVN(Open Virtual Network) (3) | 2020.07.22 |
|---|---|
| SDN - Software Defined Network (2) | 2020.07.17 |
| How to operate containerized OpenStack (1) | 2019.10.02 |
| Http 보안 및 용어 정리 (3) | 2019.09.30 |
| OpenStack Container (1) | 2019.06.07 |
- Total
- Today
- Yesterday
- 오픈스택
- openstack
- OVN
- Redhat
- ubuntu
- 우분투
- 클라우드
- 김미경
- Network
- sdn
- 쿠버네티스
- 명령어
- command
- Java
- cpu
- 컨테이너
- 파이썬
- 오픈쉬프트
- Swift
- 설치
- NOVA
- Python
- 레드햇
- 네트워크
- install
- 하둡
- 후기
- 뉴트론
- neutron
- 세미나
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
